We propose a simple method for creating photonic bose – einstein
Presented the first model describing the capture and retention of light in a state of a Bose – Einstein working flawlessly already under normal conditions.
In general, the particles can be divided into fermions and bosons (with half-integer spin and integer value). When you chill bosons to temperatures close to absolute zero, they can condense into a collective state of matter known as a Bose – Einstein condensate , when a fairly large number of atoms is in the identical quantum state that allows you to monitor various unusual phenomena like superconductivity same.
The first experience on obtaining condensate dealt with rubidium atoms cooled to near absolute zero. Left – the data on the distribution of velocities of the atoms to condensation in the center – right after, right – after a while. (Fig. R. Zhang.)
From the theoretical postulation of condensate in 1925 to its first detection in the laboratory 60 years have passed, but to conquer all peaks associated with this phenomenon is still very far away. In particular, the condensate is obtained on the basis of rubidium atoms in a gaseous state, although it would be far better to deal with photons. In addition to purely theoretical value, such a result could find and use – in lasers with unusual properties or even new types of solar cells.
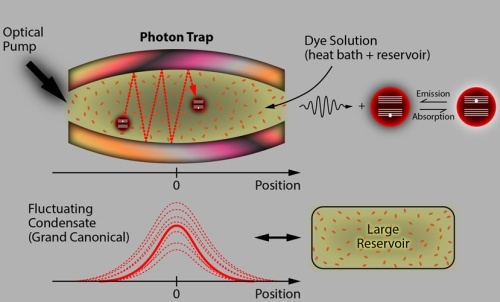
But can the photons “condense”? Light particles have no mass, and in fact it seems the presence of a key requirement for Bose – Einstein. To overcome this difficulty, physicists have tried to hold the light in an optical cavity between two parallel reflective plates that would make photons behave as if they have mass. That light is not “funneling” of such a trap, its walls should be carried slightly curved.
In 2010, it was experimentally shown that the establishment of such a trap is quite real, but remained serious problems with the interpretation of the results of such experiments. To be sure of them, it was necessary to perform several specific requirements. First, the entire system should be two-dimensional, completely flat, which is very difficult to realize three-dimensional world. Secondly, we need confidence that the medium between the photons (which is not the air) does not affect their “condensation” when cooled.
Therefore Alexey Kryuchkov from the Swiss Polytechnic School in Lausanne has developed a new mathematical model that describes the processes of “condensation” of light particles in three dimensions and in real environment. For this, he took into account the influence of the environment on the behavior of the optical cavity photons trapped there and introduced to the model of the Bose-Einstein condensate for 3D-conditions. Most importantly, his theoretical model of photon condensation corresponds to measurements obtained during the experiments. In addition, it showed that light energy can actually be accumulated in such a condensate.
The general scheme of the previously proposed optical traps suitable for making photonic “condensate” (Ill. J. Schmit).
In fact, the model suggests a more complete theory of photonic Bose – Einstein, creating a new direction in modern physics. The phenomenon, according to Mr. Kryuchkov, can be observed at room temperature (as in the experiments in 2010), making it much more affordable in the technical sense, than those ultra-low temperatures at which the Bose – Einstein condensate occurs in helium-4 or atoms undergoing laser cooling, like the same rubidium.
It is due to the absence of low temperatures suggest that the phenomenon of the same degree of singularity as superfluidity and the like, can now be used in the short-wavelength (X-ray?) Lasers, a new generation, and perhaps, in solar cells, to “condense” the incoming solar light and thus minimize its loss during conversion to electricity.
Remains unclear just this: is it possible in a single optical resonator to get more than one type of photon “condensation”? If possible, the general features of such systems can be even greater than thought.
Study report will soon appear in the journal Physical Review A , but with his preprint is available here .
Adapted from the Swiss Polytechnic School in Lausanne .